TECHNOLOGY
背景
优化问题几乎在每一个科学、商业和技术分支都存在着广泛的应用。优化问题研究如何以最佳的方式来解决实际生活中的问题,因而在实用上有着广泛应用。事实上,大部分的定量性问题求解,如科学,工程和经济学上的生产决策,设计、操作、规划和调度等都可以理解为求解相应的非线性优化问题。
一般而言,一个非线性优化问题的整体性能(或者度量)是由一个多变数的函数来描述的,称之为目标函数。根据这个通用的描述,要寻找优化问题的一个最佳解,就是需要在搜索空间寻找一个满足所有约束条件并同时使得目标函数值最小(或者最大)的向量。如果存在一个这样的向量,则称之为全域最优解。
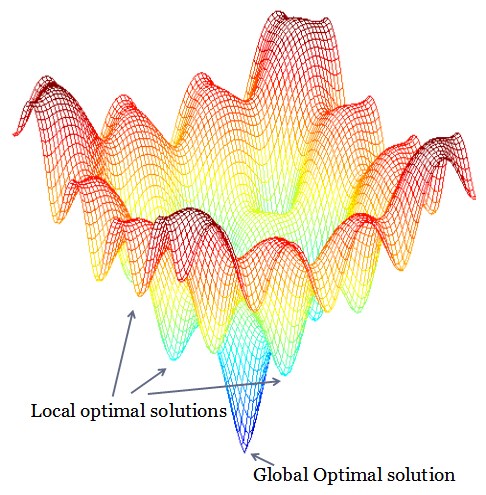
例如,全域最小解是指在整个解空间中使得目标函数值为最小的解。另一方面,一个局部最优解仅仅能保证在该解附件的一个邻域内使得目标函数值为最小。每一个局部最优解通常都有不同的目标函数值。非线性优化问题的搜索空间通常只存在有一个全域最优解和许多个局部最优解。而一般情况下,局部最优解的数目是未知的,并且这个数目可能会十分巨大,而且随着优化问题的维数扩大而增加。此外,局部最优解处的目标函数值和全域最优解处的目标函数值会有显着的不同。因此,从实际的角度出发,很有必要发展一个有效的方法来寻找全域最优解。总之,与其他可以替代的解决方案相比,全域最优解对应的方案是价值最高的。
从实用的角度来看,有很强的动机去制定有效方法来寻找全域最优解. 例如,基于全域最优解的IC设计可得到最小的IC尺寸,或是制造 IC 最廉价的生产成本,或是制造出最低功耗的IC。比较地来说,获取局部最优解的价值是不那么具有吸引力的。在激烈的竞争和全球市场行销的时代,採用全域优化技术可以让您的公司具有竞争优势,这个优势可被证明是不仅为了生存而且更为了繁荣发展的最佳战略之一。
"Nothing happens in the universe that does not have a sense of either certain maximum or minimum." - Leonhard Euler

