TECHNOLOGY
TRUST-TECH Methodology

After significant research and development efforts, we at GOT, Inc. have developed an innovative and dynamic methodology, called TRUST-TECH, to find all the local optimal solutions of general nonlinear optimization problems (two U.S. patents awarded, and 3 patents pending). Our methodology is rooted in our belief that the only reliable way to find the global optimal solution is to first find all the local optimal solutions and then find from them the global optimal solution.
Our methodology is a global optimization methodology for finding the global optimal solution by searching and screening. It is based on the theory of stability regions with mathematically rigorous foundations. TRUST-TECH is trying to develop a new pattern of correlation, namely, a better solution can be found by the present optimization technology. Thus, it avoids wasting the resources and shortens the length of study process, at the same time improves the searching methodology.
Our methodology can find all the local optimal solutions in a systematic way. Since the number of local optimal solutions can be very large and finding all of them can be a computation-intensive task, our methodology enables an effective way to first find multiple tier-by-tier local optimal solutions and then select, from them, the best solution. The capability to find a set of tier-by-tier local optimal solutions in a deterministic manner is one distinguishing feature of our methodology.
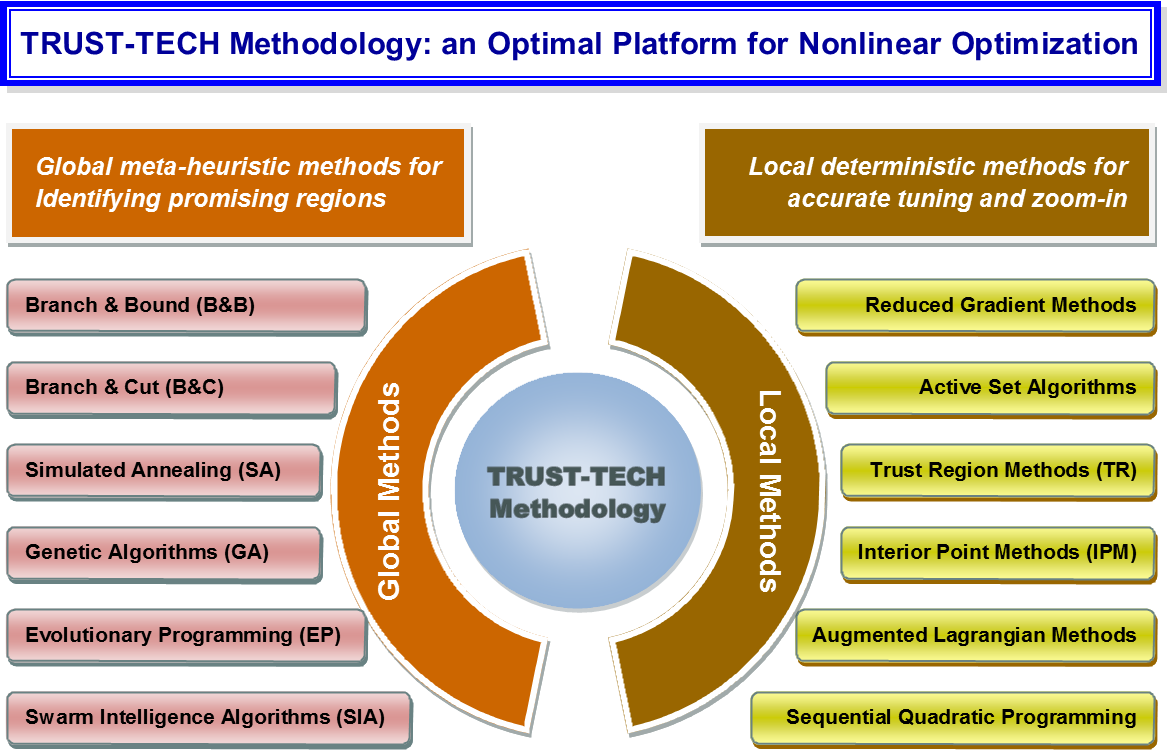
To find each local optimal solution, we believe the most effective method is a tailored 'local' optimization method that is a blend of domain knowledge and heuristics. Our innovative methodology is built on the platform where it is easy and straightforward to incorporate and use any tailored local optimization method to find local optimal solutions and find them effectively. The application scope of our dynamical methodology is very broad.
To achieve high-performance computation, we have developed several effective schemes and incorporated them into our dynamic methodology to address the following four important and challenging issues in the course of searching for the global optimal solution: (1) how to effectively move (escape) from a local optimal solution and move on toward another local optimal solution; (2) how to avoid revisiting local optimal solutions which are already found before; (3) how to identify the regions that contain local optimal solutions; and (4) how to avoid searching the regions that contain no local optimal solutions. In the past, significant efforts have been directed towards attempting to address these issues, but without much success. Issues (1) and (3) are difficult to solve and the existing methods all encounter these difficulties. Issues (2) and (4), related to computational efficiency during the course of search, are also difficult to solve and, again, the majority of existing methods all encounter these difficulties which cause the searching process into the regions of 'n'owhere' (no local optimal solutions) or into the re-visitation of same local optimal solutions several times.
GOT is based on TRUST-TECH methodology to solve varieties of optimization problems in science research and technology. We are committed to several national '985' and '973' projects and the popularization of TRUST-TECH methodology in the practical applications. GOT Technology provides a TRUST-TECH-based comprehensive platform for solving a wide-range of optimization problems.
- TRUST-TECH distinguishes itself from other global optimization methods with following unique features:
- It is deterministic in nature.
- It can converge to the global optimal solution or high-quality local optimal solutions very fast.
- It realizes a tier-by-tier global search in a transformed dynamical space.
- It can compute a comprehensive set of high-quality local optimal solutions, if not the global optimal solution.
- It provides mechanism for divergence diagnosis to pinpoint underlying causes of non-convergent problems.
- It provides mechanism for feasibility restoration, featuring optimal adjustments for infeasible conditions.
- It provides an optimal platform for incorporating local methods and global meta-heuristic methods.
- It is scalable for solving large-scale nonlinear optimization problems.