TECHNOLOGY
BACKGROUND
Optimization technology has practical applications in almost every branch of science, business and technology. It can be defined as the science of determining the `best` solution to certain mathematically defined problems, which are often models of physical reality. Optimization technology deals with how to do things in the best possible manner to solve real-life problems. There are many diverse practical applications of the technology. Indeed, a large variety of the quantitative issues such as decision-making, design, operation, planning, and scheduling arising in science, engineering, and economics can be perceived and modeled as nonlinear optimization problems.
Typically, the overall performance (or measure) of a nonlinear optimization problem is described by a multivariate function, called the objective function. According to this generic description, one seeks the best solution of an optimization problem, often expressed by a real vector, in the solution space (or search space) which satisfies all stated feasibility constraints and minimizes (or maximizes) the value of an objective function. The vector, if it exists, is termed the "global optimal solution".
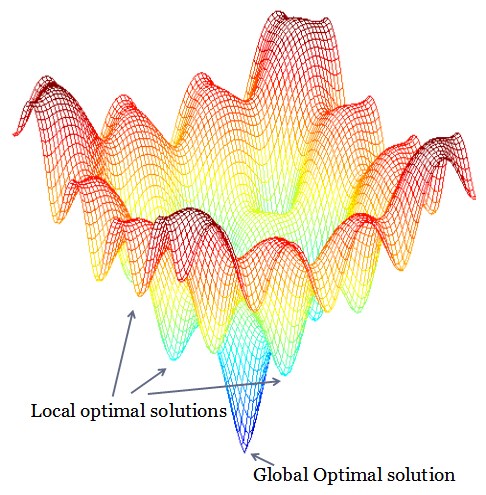
For example, a global minimum solution is the vector in the solution space that the objective function takes on its lowest value at that solution no matter where else one may search in the solution space. On the other hand, a local optimal solution only guarantees that its objective function value is a minimum with respect to other points nearby in the solution space. Each local optimal solution has a different value of the objective function. The solution space (i.e. search space) of nonlinear optimization problems generally contains only one global optimal solution and many local optimal solutions. Typically, the number of local optimal solutions is unknown and it can be quite large and grows significantly with the dimension of solution space. Furthermore, the values of an objective function at local optimal solutions and at the global optimal solution may differ significantly. Hence, from a practical viewpoint, there are strong motivations to develop effective methods for finding the global optimal solution. The value of obtaining the global optimal solution is highest when compared to alternative solutions.
From a practical viewpoint, there are strong motivations to develop effective methods for finding the global optimal solution. For example, IC design based on the global optimal solution leads to the smallest size of IC, or to the cheapest production cost of manufacturing IC or IC’s with the lowest power consumption. Comparatively speaking, the value of obtaining local optimal solutions is less attractive. During the era of intense competition and global marketing, adopting global optimal technology can give your company the competitive advantage that may prove to be one of the best strategies for not only survival but also prosperity.
"Nothing happens in the universe that does not have a sense of either certain maximum or minimum." - Leonhard Euler

